We are using cookies
This website uses cookies in order to offer you the most relevant information. By browsing this website, you accept these cookies.
This website uses cookies in order to offer you the most relevant information. By browsing this website, you accept these cookies.
Did you know?
You can double click on a word to look it up on TermGallery.
You can double click on a word to look it up on TermGallery.
Meanings of cosine in английском
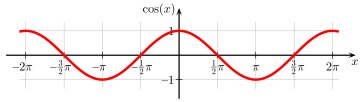
Trigonometric function; ratio between the lengths of the adjacent side and the hypotenuse in a right triangle.
Related terms
Usage of cosine in английском
1
Go ahead and solve the above expression for the cosine of θ.
2
Two functions that meet those requirements are the sine and cosine functions.
3
I have never used a sine or cosine in my everyday life.
4
In y-equation, it has the sin of θ but I have cosine.
5
See, this triangle has the same value for cosine of θ.
6
Using the sum of angles formula to evaluate the cosine is a mathematical exercise.
7
C-squared equals a-squared plus b-squared minus 2 times a-b times the cosine of angle C.
8
A cosine is the adjacent divided by the hypotenuse.
9
The results support possible roles for leaky integration and cosine-shaped compass response functions in path integration.
10
How does a calculator evaluate the cosine function?
11
A cosine function within a 24-h period was used to characterize daily rhythms using a random regression.
12
We also applied the concept of cosine similarity to confidently infer the associations between diseases and genes.
13
The sine and cosine coefficients of the first harmonic are extracted from the gated views and reconstructed.
14
The cosine of 90 degrees is zero.
15
He invented tools for computation, navigation and surveying, and invented the trigonometry concepts of cosine and cotangent.
16
Does everyone need to know what a cosine is if the UK is to have a brighter future?
About this term
Frequent collocations
Cosine through the time